A Regularized Adjusted Plus-Minus Model in Soccer

.title[
# <strong>A Regularized Adjusted Plus-Minus Model in Soccer</strong>
]
.subtitle[
## <strong>with Box Score Prior</strong>
]
.author[
### <strong>Boyuan Zhang (New York University)</strong>
]
.institute[
### <br />Collaborators: Phong Hoang (Denison), Edvin Tran Hoac (Wesleyan)
]
.institute[
### Advisors: Prof. Kostas Pelechrinis (UPitt), Prof. Ron Yurko (CMU)
]
.date[
### <br />Carnegie Mellon Sports Analytics Conference<br />October 29, 2022
]

---

# How to evaluate the impact of individual players on their team’s performance within a period of time?

---

# Plus-Minus (+/-) Model

## Concept:

keeps track of the net changes in the score when a given player is either on or off the court

## Formula:

.center[**Plus-Minus for Any Player = (Team Points Scored - Team Points Allowed) While That Player is On The Court**]

## Benefits:

- Identify a player’s implied effect on his team’s goal difference while he is on the field
  - Data required to compute Plus-Minus are already available: only need the player lineups and substitutions records with the times at which they occurred, and goals scored and their corresponding times
  - Could be employed in any league, on any match, at any time

## Problems:
  - A player’s effect on his team’s goal differential will change as the makeup of teammates and opponents changes during the game

---

# Adjusted Plus-Minus (APM) Model

## Concept:

Over a given time period, adjusting the basic plus-minus results to account for both the teammates and the opponents on the court.

## Formula:

`$$\frac{T_{total}}{T_{j}} \Delta S = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_ix_i + \cdots + \beta_nx_n + \epsilon$$`
  - `$\Delta S$`: Score differential, `$S_{home} - S_{away}$`
  - `$T_j$`: Length of time segment, the interval in which no substitutions or expulsions occurred, for `$j = 1, \dots, R$` segments
  - `$\beta_0$`: Average home team advantage over all teams in the competition
  - `$\beta_i$`: Influence of player `$i$` on goal differential, for `$i = 1, \dots, N$` players in competition
  - `$x_i$`: Player appearance index:
    - +1: Player `$i$` is playing at home
    - 0: Player `$i$` is not playing
    - -1: Player `$i$` is playing away

---

# Adjusted Plus-Minus (APM) Model

`$$\beta^* = \arg \min_{\beta} ||\Delta S - tX\beta||_2^2$$`

## Interpretation:
APM ratings indicate how many additional points are contributed to a team’s scoring margin by a given player in comparison to the league-average player whose APM value is zero over the span of a typical game.

## Benefits:

- Reflects the impact of each player on his team’s scoring margin after controlling for the strength of every teammate and every opponent during each minute he’s on the court

## Problems:
  - High variance, overfitting, and sensitive to the noise
  - Multicollinearity: Coaches prefer to use some groups of players more frequently or rarely since all players could not be on the court with every other teammate at the same time

---

# Regularized Adjusted Plus-Minus (RAPM) Model

## Concept:

Adding regularization into APM model to improve model accuracy.

## Formula:

`$$\beta^* = \arg \min_{\beta} ||\Delta S - tX\beta||_2^2 + \lambda||\beta||_2^2$$`

## Benefits:

- Significantly reduces standard errors in APM model and provide more accurate prediction results

## Problems:

- Multicollinearity: Coaches prefer to use some groups of players more frequently or rarely since all players could not be on the court with every other teammate at the same time

---

# Problematic Nature of Soccer

<div class="figure" style="text-align: center">
<img src="https://www.intraocular.net/posts/how-augmented-apm-works/scoring_vs_subs_sports-1.png" alt="Matano, et al (2018). Augmenting adjusted plus-minus in soccer with FIFA ratings." width="50%" height="50%" />
<p class="caption">Matano, et al (2018). Augmenting adjusted plus-minus in soccer with FIFA ratings.</p>
</div>

- Low number of substitutions `$\Longrightarrow$` multicollinearity between features
- Low number of scoring `$\Longrightarrow$` sparse response variable

---

# Current State of Socceer Player Rating

## Action-based Player Ratings

---

# Current State of Socceer Player Rating

## Video Game Player Ratings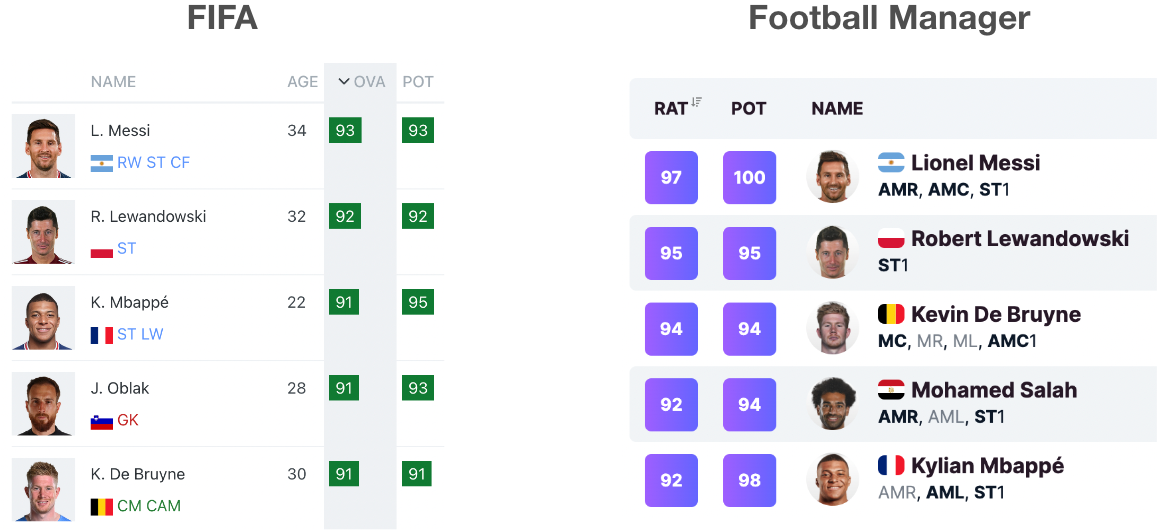

---

# Current State of Socceer Player Rating

Matano, F., L. F. Richardson, T. Pospisil, C. Eubanks, and J. Qin (2018): “[`Augmenting Adjusted Plus-Minus in Soccer with FIFA Ratings`](https://arxiv.org/abs/1810.08032),” _Carnegie Mellon Sports Analytics Conference_.

- Recasting APM into a Bayesian framework, and incorporating FIFA ratings into the prior distribution
- Shown that Argumented APM predicts better than standard APM and a model using only FIFA ratings
- Shown that Agumented APM decorrelates players that are highly collinear

---

# RAxGPM with Box Score Prior

## Previous Formula:

`$$\beta^* = \arg \min_{\beta} ||\Delta G - tX\beta||_2^2 + \lambda||\beta||_2^2$$`
## New Formula:

`$$\beta^* = \arg \min_{\beta} ||\Delta \mathbb{xG} - tX\beta||_2^2 + \lambda||\beta - \beta_{prior}||_2^2$$`
  - `$\Delta \mathbb{xG}$`: Expected Goal differential, `$\mathbb{xG}_{home} - \mathbb{xG}_{away}$`
  - `$\beta_{prior}$`: Prior value for each player learned from **box score data**

## Idea:

- More frequent response variable
  - Less collinearity between players

---

# Model Pipelin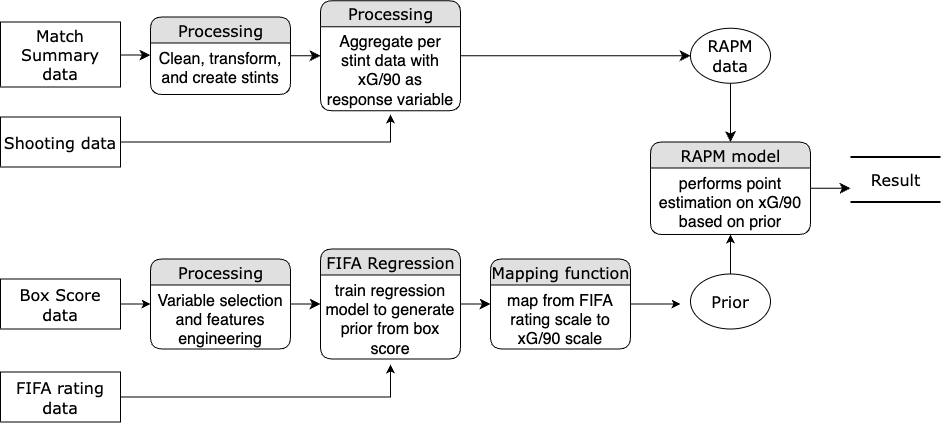e

---

# Example: English Premier League 2021-22 Season

---

# Data: Prior Stage

## Box Score Data: EPL season 2020-21 and 2021-22
- 3,420 observations and more than 180 features
- only consider player with 900 minutes and above in corresponding season
- after variable selection, around 30 features are left including the following criteria: 
  - Scoring, creating, dribbling, passing and defensive actions, etc.

## FIFA Ratings 2022 Data: before starts of 2021-22 season
- only collected one overall rating for each unique player

---

# Data: Prior Stage

## Number of Players by Position Group

---

# Model Training: Prior

## Feature Importance in Prior Value by Position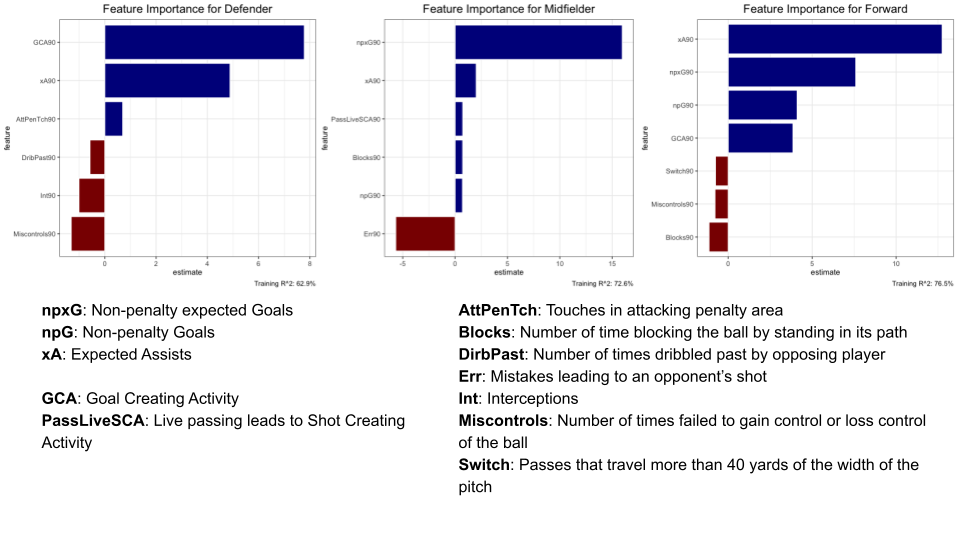

---

# Model Training: Prior

## Comparing between FIFA rating and Prior value distribution

---

# Data: RAPM Stage

## Match Summary data: EPL season 2021-22
  - collected line-ups, substitutions, and every events for every game
  - create stint with time start and length: 
    - a stint is created when there is a substitution, a red card, or a goal happens
  - 4000 stints over 380 matches

## Shooting Data: EPL season 2021-22
  - collected shooting information with corresponding expected goals for every shot in the season

---

# Data: RAPM Stage

## Match Summary data: EPL season 2021-22

---

# Data: RAPM Stage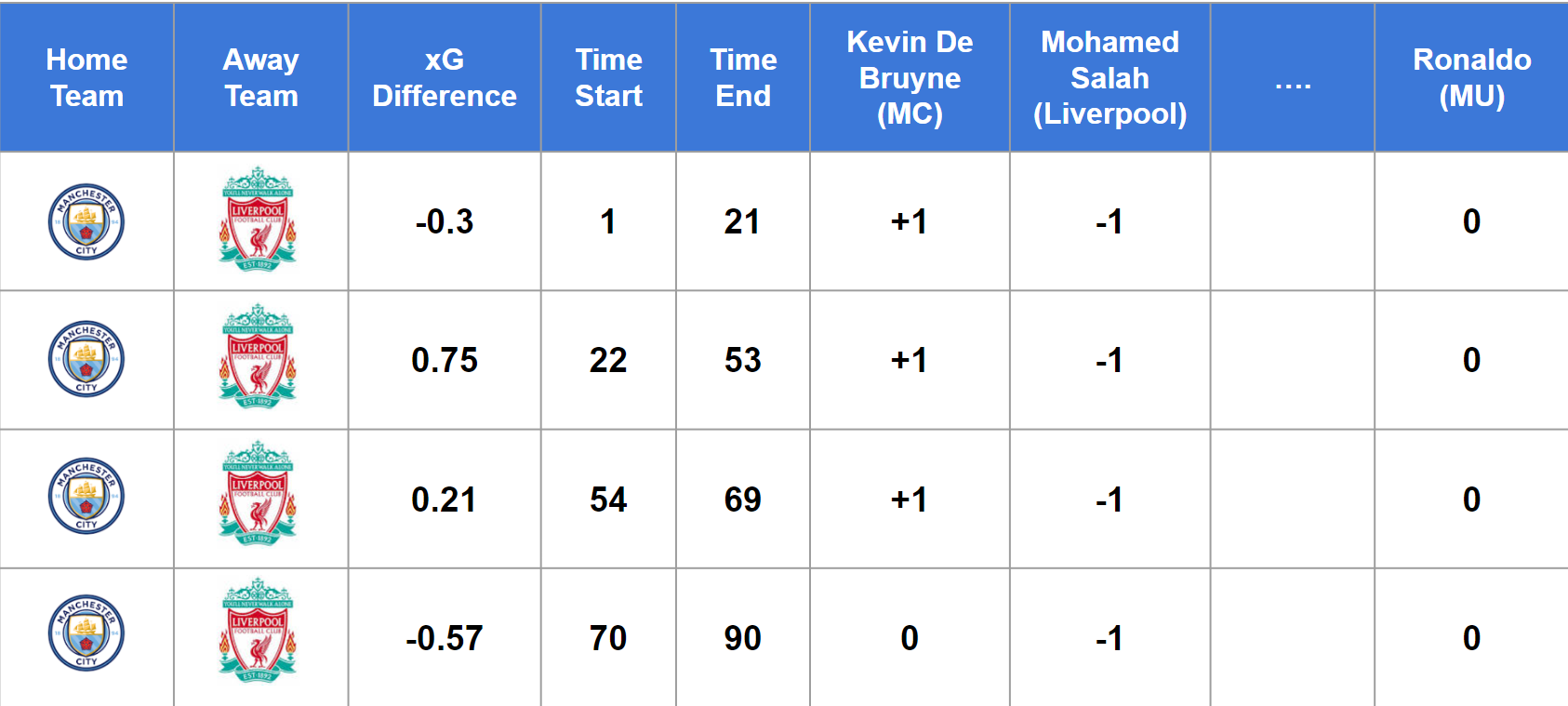

---

# Model Training: RAPM

---

# Model Training: RAPM

---

# Model Testing: Predictability

---

# Model Testing: Predictability

10-fold cross-validation with accuracy measured by RMSE:
  - **RAPM_only**: RAPM model without any prior
  - **RAPM_FIFA**: RAPM model with FIFA rating directly as prior
  - **RAPM_box**: RAPM model with prior created from box score data

---

# Result: Top 10 Players

<div id="jozrgespzo" style="overflow-x:auto;overflow-y:auto;width:auto;height:auto;">
<style>html {
  font-family: -apple-system, BlinkMacSystemFont, 'Segoe UI', Roboto, Oxygen, Ubuntu, Cantarell, 'Helvetica Neue', 'Fira Sans', 'Droid Sans', Arial, sans-serif;
}

#jozrgespzo .gt_table {
  display: table;
  border-collapse: collapse;
  margin-left: auto;
  margin-right: auto;
  color: #333333;
  font-size: 16px;
  font-weight: normal;
  font-style: normal;
  background-color: #FFFFFF;
  width: auto;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #A8A8A8;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #A8A8A8;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
}

#jozrgespzo .gt_heading {
  background-color: #FFFFFF;
  text-align: center;
  border-bottom-color: #FFFFFF;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
}

#jozrgespzo .gt_title {
  color: #333333;
  font-size: 125%;
  font-weight: initial;
  padding-top: 4px;
  padding-bottom: 4px;
  padding-left: 5px;
  padding-right: 5px;
  border-bottom-color: #FFFFFF;
  border-bottom-width: 0;
}

#jozrgespzo .gt_subtitle {
  color: #333333;
  font-size: 85%;
  font-weight: initial;
  padding-top: 0;
  padding-bottom: 6px;
  padding-left: 5px;
  padding-right: 5px;
  border-top-color: #FFFFFF;
  border-top-width: 0;
}

#jozrgespzo .gt_bottom_border {
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#jozrgespzo .gt_col_headings {
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
}

#jozrgespzo .gt_col_heading {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: normal;
  text-transform: inherit;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: bottom;
  padding-top: 5px;
  padding-bottom: 6px;
  padding-left: 5px;
  padding-right: 5px;
  overflow-x: hidden;
}

#jozrgespzo .gt_column_spanner_outer {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: normal;
  text-transform: inherit;
  padding-top: 0;
  padding-bottom: 0;
  padding-left: 4px;
  padding-right: 4px;
}

#jozrgespzo .gt_column_spanner_outer:first-child {
  padding-left: 0;
}

#jozrgespzo .gt_column_spanner_outer:last-child {
  padding-right: 0;
}

#jozrgespzo .gt_column_spanner {
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  vertical-align: bottom;
  padding-top: 5px;
  padding-bottom: 5px;
  overflow-x: hidden;
  display: inline-block;
  width: 100%;
}

#jozrgespzo .gt_group_heading {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: middle;
}

#jozrgespzo .gt_empty_group_heading {
  padding: 0.5px;
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  vertical-align: middle;
}

#jozrgespzo .gt_from_md > :first-child {
  margin-top: 0;
}

#jozrgespzo .gt_from_md > :last-child {
  margin-bottom: 0;
}

#jozrgespzo .gt_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  margin: 10px;
  border-top-style: solid;
  border-top-width: 1px;
  border-top-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: middle;
  overflow-x: hidden;
}

#jozrgespzo .gt_stub {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-right-style: solid;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  padding-left: 5px;
  padding-right: 5px;
}

#jozrgespzo .gt_stub_row_group {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-right-style: solid;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  padding-left: 5px;
  padding-right: 5px;
  vertical-align: top;
}

#jozrgespzo .gt_row_group_first td {
  border-top-width: 2px;
}

#jozrgespzo .gt_summary_row {
  color: #333333;
  background-color: #FFFFFF;
  text-transform: inherit;
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
}

#jozrgespzo .gt_first_summary_row {
  border-top-style: solid;
  border-top-color: #D3D3D3;
}

#jozrgespzo .gt_first_summary_row.thick {
  border-top-width: 2px;
}

#jozrgespzo .gt_last_summary_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#jozrgespzo .gt_grand_summary_row {
  color: #333333;
  background-color: #FFFFFF;
  text-transform: inherit;
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
}

#jozrgespzo .gt_first_grand_summary_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  border-top-style: double;
  border-top-width: 6px;
  border-top-color: #D3D3D3;
}

#jozrgespzo .gt_striped {
  background-color: rgba(128, 128, 128, 0.05);
}

#jozrgespzo .gt_table_body {
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#jozrgespzo .gt_footnotes {
  color: #333333;
  background-color: #FFFFFF;
  border-bottom-style: none;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
}

#jozrgespzo .gt_footnote {
  margin: 0px;
  font-size: 90%;
  padding-left: 4px;
  padding-right: 4px;
  padding-left: 5px;
  padding-right: 5px;
}

#jozrgespzo .gt_sourcenotes {
  color: #333333;
  background-color: #FFFFFF;
  border-bottom-style: none;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
}

#jozrgespzo .gt_sourcenote {
  font-size: 90%;
  padding-top: 4px;
  padding-bottom: 4px;
  padding-left: 5px;
  padding-right: 5px;
}

#jozrgespzo .gt_left {
  text-align: left;
}

#jozrgespzo .gt_center {
  text-align: center;
}

#jozrgespzo .gt_right {
  text-align: right;
  font-variant-numeric: tabular-nums;
}

#jozrgespzo .gt_font_normal {
  font-weight: normal;
}

#jozrgespzo .gt_font_bold {
  font-weight: bold;
}

#jozrgespzo .gt_font_italic {
  font-style: italic;
}

#jozrgespzo .gt_super {
  font-size: 65%;
}

#jozrgespzo .gt_footnote_marks {
  font-style: italic;
  font-weight: normal;
  font-size: 75%;
  vertical-align: 0.4em;
}

#jozrgespzo .gt_asterisk {
  font-size: 100%;
  vertical-align: 0;
}

#jozrgespzo .gt_indent_1 {
  text-indent: 5px;
}

#jozrgespzo .gt_indent_2 {
  text-indent: 10px;
}

#jozrgespzo .gt_indent_3 {
  text-indent: 15px;
}

#jozrgespzo .gt_indent_4 {
  text-indent: 20px;
}

#jozrgespzo .gt_indent_5 {
  text-indent: 25px;
}
</style>
<table class="gt_table">
  
  <thead class="gt_col_headings">
    <tr>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col"></th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Player</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Team</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Pos</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">Min</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">FIFA</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">FIFA_rating</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">Box</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">box_rating</th>
    </tr>
  </thead>
  <tbody class="gt_table_body">
    <tr><th scope="row" class="gt_row gt_right gt_stub">1</th>
<td class="gt_row gt_left">Mohamed Salah</td>
<td class="gt_row gt_left">Liverpool</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2762</td>
<td class="gt_row gt_right">89</td>
<td class="gt_row gt_right" style="background-color: rgba(171,138,193,0.8); color: #000000;">0.12174911</td>
<td class="gt_row gt_right">90.13389</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">0.1497441</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">2</th>
<td class="gt_row gt_left">Reece James</td>
<td class="gt_row gt_left">Chelsea</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">1864</td>
<td class="gt_row gt_right">81</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">0.02262148</td>
<td class="gt_row gt_right">87.35088</td>
<td class="gt_row gt_right" style="background-color: rgba(216,196,228,0.8); color: #000000;">0.1168662</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">3</th>
<td class="gt_row gt_left">İlkay Gündoğan</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">1857</td>
<td class="gt_row gt_right">85</td>
<td class="gt_row gt_right" style="background-color: rgba(215,195,227,0.8); color: #000000;">0.07182136</td>
<td class="gt_row gt_right">87.76583</td>
<td class="gt_row gt_right" style="background-color: rgba(217,197,228,0.8); color: #000000;">0.1142307</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">4</th>
<td class="gt_row gt_left">Sadio Mané</td>
<td class="gt_row gt_left">Liverpool</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2819</td>
<td class="gt_row gt_right">89</td>
<td class="gt_row gt_right" style="background-color: rgba(181,149,202,0.8); color: #000000;">0.11953468</td>
<td class="gt_row gt_right">87.65664</td>
<td class="gt_row gt_right" style="background-color: rgba(221,203,231,0.8); color: #000000;">0.1121862</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">5</th>
<td class="gt_row gt_left">João Cancelo</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">3227</td>
<td class="gt_row gt_right">86</td>
<td class="gt_row gt_right" style="background-color: rgba(215,195,228,0.8); color: #000000;">0.06593877</td>
<td class="gt_row gt_right">88.39155</td>
<td class="gt_row gt_right" style="background-color: rgba(232,220,239,0.8); color: #000000;">0.1061954</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">6</th>
<td class="gt_row gt_left">Paul Pogba</td>
<td class="gt_row gt_left">Manchester Utd</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">1349</td>
<td class="gt_row gt_right">87</td>
<td class="gt_row gt_right" style="background-color: rgba(200,171,217,0.8); color: #000000;">0.11021187</td>
<td class="gt_row gt_right">86.09682</td>
<td class="gt_row gt_right" style="background-color: rgba(232,221,239,0.8); color: #000000;">0.1060792</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">7</th>
<td class="gt_row gt_left">Harry Kane</td>
<td class="gt_row gt_left">Tottenham</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">3232</td>
<td class="gt_row gt_right">90</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">0.14763053</td>
<td class="gt_row gt_right">86.78122</td>
<td class="gt_row gt_right" style="background-color: rgba(236,227,242,0.8); color: #000000;">0.1040146</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">8</th>
<td class="gt_row gt_left">Son Heung-min</td>
<td class="gt_row gt_left">Tottenham</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">3006</td>
<td class="gt_row gt_right">89</td>
<td class="gt_row gt_right" style="background-color: rgba(115,76,148,0.8); color: #FFFFFF;">0.13393589</td>
<td class="gt_row gt_right">86.69345</td>
<td class="gt_row gt_right" style="background-color: rgba(236,227,242,0.8); color: #000000;">0.1037975</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">9</th>
<td class="gt_row gt_left">Alisson</td>
<td class="gt_row gt_left">Liverpool</td>
<td class="gt_row gt_left">GK</td>
<td class="gt_row gt_right">3240</td>
<td class="gt_row gt_right">89</td>
<td class="gt_row gt_right" style="background-color: rgba(198,169,215,0.8); color: #000000;">0.11339948</td>
<td class="gt_row gt_right">87.27274</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">0.1029704</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">10</th>
<td class="gt_row gt_left">Phil Foden</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2128</td>
<td class="gt_row gt_right">84</td>
<td class="gt_row gt_right" style="background-color: rgba(219,200,230,0.8); color: #000000;">0.05020127</td>
<td class="gt_row gt_right">87.30791</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">0.1029035</td></tr>
  </tbody>
  
  
</table>
</div>

---

# Result: Top 10-20 Players

<div id="nkvnfhqxfk" style="overflow-x:auto;overflow-y:auto;width:auto;height:auto;">
<style>html {
  font-family: -apple-system, BlinkMacSystemFont, 'Segoe UI', Roboto, Oxygen, Ubuntu, Cantarell, 'Helvetica Neue', 'Fira Sans', 'Droid Sans', Arial, sans-serif;
}

#nkvnfhqxfk .gt_table {
  display: table;
  border-collapse: collapse;
  margin-left: auto;
  margin-right: auto;
  color: #333333;
  font-size: 16px;
  font-weight: normal;
  font-style: normal;
  background-color: #FFFFFF;
  width: auto;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #A8A8A8;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #A8A8A8;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
}

#nkvnfhqxfk .gt_heading {
  background-color: #FFFFFF;
  text-align: center;
  border-bottom-color: #FFFFFF;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
}

#nkvnfhqxfk .gt_title {
  color: #333333;
  font-size: 125%;
  font-weight: initial;
  padding-top: 4px;
  padding-bottom: 4px;
  padding-left: 5px;
  padding-right: 5px;
  border-bottom-color: #FFFFFF;
  border-bottom-width: 0;
}

#nkvnfhqxfk .gt_subtitle {
  color: #333333;
  font-size: 85%;
  font-weight: initial;
  padding-top: 0;
  padding-bottom: 6px;
  padding-left: 5px;
  padding-right: 5px;
  border-top-color: #FFFFFF;
  border-top-width: 0;
}

#nkvnfhqxfk .gt_bottom_border {
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#nkvnfhqxfk .gt_col_headings {
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
}

#nkvnfhqxfk .gt_col_heading {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: normal;
  text-transform: inherit;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: bottom;
  padding-top: 5px;
  padding-bottom: 6px;
  padding-left: 5px;
  padding-right: 5px;
  overflow-x: hidden;
}

#nkvnfhqxfk .gt_column_spanner_outer {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: normal;
  text-transform: inherit;
  padding-top: 0;
  padding-bottom: 0;
  padding-left: 4px;
  padding-right: 4px;
}

#nkvnfhqxfk .gt_column_spanner_outer:first-child {
  padding-left: 0;
}

#nkvnfhqxfk .gt_column_spanner_outer:last-child {
  padding-right: 0;
}

#nkvnfhqxfk .gt_column_spanner {
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  vertical-align: bottom;
  padding-top: 5px;
  padding-bottom: 5px;
  overflow-x: hidden;
  display: inline-block;
  width: 100%;
}

#nkvnfhqxfk .gt_group_heading {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: middle;
}

#nkvnfhqxfk .gt_empty_group_heading {
  padding: 0.5px;
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  vertical-align: middle;
}

#nkvnfhqxfk .gt_from_md > :first-child {
  margin-top: 0;
}

#nkvnfhqxfk .gt_from_md > :last-child {
  margin-bottom: 0;
}

#nkvnfhqxfk .gt_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  margin: 10px;
  border-top-style: solid;
  border-top-width: 1px;
  border-top-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: middle;
  overflow-x: hidden;
}

#nkvnfhqxfk .gt_stub {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-right-style: solid;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  padding-left: 5px;
  padding-right: 5px;
}

#nkvnfhqxfk .gt_stub_row_group {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-right-style: solid;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  padding-left: 5px;
  padding-right: 5px;
  vertical-align: top;
}

#nkvnfhqxfk .gt_row_group_first td {
  border-top-width: 2px;
}

#nkvnfhqxfk .gt_summary_row {
  color: #333333;
  background-color: #FFFFFF;
  text-transform: inherit;
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
}

#nkvnfhqxfk .gt_first_summary_row {
  border-top-style: solid;
  border-top-color: #D3D3D3;
}

#nkvnfhqxfk .gt_first_summary_row.thick {
  border-top-width: 2px;
}

#nkvnfhqxfk .gt_last_summary_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#nkvnfhqxfk .gt_grand_summary_row {
  color: #333333;
  background-color: #FFFFFF;
  text-transform: inherit;
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
}

#nkvnfhqxfk .gt_first_grand_summary_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  border-top-style: double;
  border-top-width: 6px;
  border-top-color: #D3D3D3;
}

#nkvnfhqxfk .gt_striped {
  background-color: rgba(128, 128, 128, 0.05);
}

#nkvnfhqxfk .gt_table_body {
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#nkvnfhqxfk .gt_footnotes {
  color: #333333;
  background-color: #FFFFFF;
  border-bottom-style: none;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
}

#nkvnfhqxfk .gt_footnote {
  margin: 0px;
  font-size: 90%;
  padding-left: 4px;
  padding-right: 4px;
  padding-left: 5px;
  padding-right: 5px;
}

#nkvnfhqxfk .gt_sourcenotes {
  color: #333333;
  background-color: #FFFFFF;
  border-bottom-style: none;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
}

#nkvnfhqxfk .gt_sourcenote {
  font-size: 90%;
  padding-top: 4px;
  padding-bottom: 4px;
  padding-left: 5px;
  padding-right: 5px;
}

#nkvnfhqxfk .gt_left {
  text-align: left;
}

#nkvnfhqxfk .gt_center {
  text-align: center;
}

#nkvnfhqxfk .gt_right {
  text-align: right;
  font-variant-numeric: tabular-nums;
}

#nkvnfhqxfk .gt_font_normal {
  font-weight: normal;
}

#nkvnfhqxfk .gt_font_bold {
  font-weight: bold;
}

#nkvnfhqxfk .gt_font_italic {
  font-style: italic;
}

#nkvnfhqxfk .gt_super {
  font-size: 65%;
}

#nkvnfhqxfk .gt_footnote_marks {
  font-style: italic;
  font-weight: normal;
  font-size: 75%;
  vertical-align: 0.4em;
}

#nkvnfhqxfk .gt_asterisk {
  font-size: 100%;
  vertical-align: 0;
}

#nkvnfhqxfk .gt_indent_1 {
  text-indent: 5px;
}

#nkvnfhqxfk .gt_indent_2 {
  text-indent: 10px;
}

#nkvnfhqxfk .gt_indent_3 {
  text-indent: 15px;
}

#nkvnfhqxfk .gt_indent_4 {
  text-indent: 20px;
}

#nkvnfhqxfk .gt_indent_5 {
  text-indent: 25px;
}
</style>
<table class="gt_table">
  
  <thead class="gt_col_headings">
    <tr>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col"></th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Player</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Team</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Pos</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">Min</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">FIFA</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">FIFA_rating</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">Box</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">box_rating</th>
    </tr>
  </thead>
  <tbody class="gt_table_body">
    <tr><th scope="row" class="gt_row gt_right gt_stub">1</th>
<td class="gt_row gt_left">Ederson</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">GK</td>
<td class="gt_row gt_right">3330</td>
<td class="gt_row gt_right">89</td>
<td class="gt_row gt_right" style="background-color: rgba(114,53,159,0.8); color: #FFFFFF;">0.10897867</td>
<td class="gt_row gt_right">88.14836</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">0.10238281</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">2</th>
<td class="gt_row gt_left">Rúben Dias</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">2402</td>
<td class="gt_row gt_right">87</td>
<td class="gt_row gt_right" style="background-color: rgba(115,59,160,0.8); color: #FFFFFF;">0.09109630</td>
<td class="gt_row gt_right">87.23700</td>
<td class="gt_row gt_right" style="background-color: rgba(110,46,155,0.8); color: #FFFFFF;">0.09924433</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">3</th>
<td class="gt_row gt_left">Rodri</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">2884</td>
<td class="gt_row gt_right">86</td>
<td class="gt_row gt_right" style="background-color: rgba(143,96,178,0.8); color: #FFFFFF;">0.07158721</td>
<td class="gt_row gt_right">87.50666</td>
<td class="gt_row gt_right" style="background-color: rgba(114,54,159,0.8); color: #FFFFFF;">0.09765550</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">4</th>
<td class="gt_row gt_left">Roberto Firmino</td>
<td class="gt_row gt_left">Liverpool</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">990</td>
<td class="gt_row gt_right">85</td>
<td class="gt_row gt_right" style="background-color: rgba(116,62,160,0.8); color: #FFFFFF;">0.08445760</td>
<td class="gt_row gt_right">85.44965</td>
<td class="gt_row gt_right" style="background-color: rgba(131,81,170,0.8); color: #FFFFFF;">0.09521369</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">5</th>
<td class="gt_row gt_left">Gabriel Jesus</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">1877</td>
<td class="gt_row gt_right">83</td>
<td class="gt_row gt_right" style="background-color: rgba(197,167,215,0.8); color: #000000;">0.04402586</td>
<td class="gt_row gt_right">86.32616</td>
<td class="gt_row gt_right" style="background-color: rgba(153,109,185,0.8); color: #000000;">0.09429259</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">6</th>
<td class="gt_row gt_left">Raheem Sterling</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2128</td>
<td class="gt_row gt_right">88</td>
<td class="gt_row gt_right" style="background-color: rgba(114,52,159,0.8); color: #FFFFFF;">0.11026872</td>
<td class="gt_row gt_right">86.64789</td>
<td class="gt_row gt_right" style="background-color: rgba(162,120,191,0.8); color: #000000;">0.09390230</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">7</th>
<td class="gt_row gt_left">Luis Díaz</td>
<td class="gt_row gt_left">Liverpool</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">958</td>
<td class="gt_row gt_right">80</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">0.01084548</td>
<td class="gt_row gt_right">85.32550</td>
<td class="gt_row gt_right" style="background-color: rgba(188,155,209,0.8); color: #000000;">0.09277333</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">8</th>
<td class="gt_row gt_left">Kevin De Bruyne</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">2201</td>
<td class="gt_row gt_right">91</td>
<td class="gt_row gt_right" style="background-color: rgba(60,12,106,0.8); color: #FFFFFF;">0.15216341</td>
<td class="gt_row gt_right">86.60226</td>
<td class="gt_row gt_right" style="background-color: rgba(194,163,213,0.8); color: #000000;">0.09247912</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">9</th>
<td class="gt_row gt_left">Cristiano Ronaldo</td>
<td class="gt_row gt_left">Manchester Utd</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2456</td>
<td class="gt_row gt_right">91</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">0.15745070</td>
<td class="gt_row gt_right">85.19735</td>
<td class="gt_row gt_right" style="background-color: rgba(212,189,225,0.8); color: #000000;">0.09123895</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">10</th>
<td class="gt_row gt_left">Aymeric Laporte</td>
<td class="gt_row gt_left">Manchester City</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">2828</td>
<td class="gt_row gt_right">86</td>
<td class="gt_row gt_right" style="background-color: rgba(146,99,180,0.8); color: #FFFFFF;">0.07031695</td>
<td class="gt_row gt_right">86.94222</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">0.08930280</td></tr>
  </tbody>
  
  
</table>
</div>

---

# Result: Bottom 10 Players

<div id="bxelbytvcn" style="overflow-x:auto;overflow-y:auto;width:auto;height:auto;">
<style>html {
  font-family: -apple-system, BlinkMacSystemFont, 'Segoe UI', Roboto, Oxygen, Ubuntu, Cantarell, 'Helvetica Neue', 'Fira Sans', 'Droid Sans', Arial, sans-serif;
}

#bxelbytvcn .gt_table {
  display: table;
  border-collapse: collapse;
  margin-left: auto;
  margin-right: auto;
  color: #333333;
  font-size: 16px;
  font-weight: normal;
  font-style: normal;
  background-color: #FFFFFF;
  width: auto;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #A8A8A8;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #A8A8A8;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
}

#bxelbytvcn .gt_heading {
  background-color: #FFFFFF;
  text-align: center;
  border-bottom-color: #FFFFFF;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
}

#bxelbytvcn .gt_title {
  color: #333333;
  font-size: 125%;
  font-weight: initial;
  padding-top: 4px;
  padding-bottom: 4px;
  padding-left: 5px;
  padding-right: 5px;
  border-bottom-color: #FFFFFF;
  border-bottom-width: 0;
}

#bxelbytvcn .gt_subtitle {
  color: #333333;
  font-size: 85%;
  font-weight: initial;
  padding-top: 0;
  padding-bottom: 6px;
  padding-left: 5px;
  padding-right: 5px;
  border-top-color: #FFFFFF;
  border-top-width: 0;
}

#bxelbytvcn .gt_bottom_border {
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#bxelbytvcn .gt_col_headings {
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
}

#bxelbytvcn .gt_col_heading {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: normal;
  text-transform: inherit;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: bottom;
  padding-top: 5px;
  padding-bottom: 6px;
  padding-left: 5px;
  padding-right: 5px;
  overflow-x: hidden;
}

#bxelbytvcn .gt_column_spanner_outer {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: normal;
  text-transform: inherit;
  padding-top: 0;
  padding-bottom: 0;
  padding-left: 4px;
  padding-right: 4px;
}

#bxelbytvcn .gt_column_spanner_outer:first-child {
  padding-left: 0;
}

#bxelbytvcn .gt_column_spanner_outer:last-child {
  padding-right: 0;
}

#bxelbytvcn .gt_column_spanner {
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  vertical-align: bottom;
  padding-top: 5px;
  padding-bottom: 5px;
  overflow-x: hidden;
  display: inline-block;
  width: 100%;
}

#bxelbytvcn .gt_group_heading {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: middle;
}

#bxelbytvcn .gt_empty_group_heading {
  padding: 0.5px;
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  vertical-align: middle;
}

#bxelbytvcn .gt_from_md > :first-child {
  margin-top: 0;
}

#bxelbytvcn .gt_from_md > :last-child {
  margin-bottom: 0;
}

#bxelbytvcn .gt_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  margin: 10px;
  border-top-style: solid;
  border-top-width: 1px;
  border-top-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 1px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 1px;
  border-right-color: #D3D3D3;
  vertical-align: middle;
  overflow-x: hidden;
}

#bxelbytvcn .gt_stub {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-right-style: solid;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  padding-left: 5px;
  padding-right: 5px;
}

#bxelbytvcn .gt_stub_row_group {
  color: #333333;
  background-color: #FFFFFF;
  font-size: 100%;
  font-weight: initial;
  text-transform: inherit;
  border-right-style: solid;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
  padding-left: 5px;
  padding-right: 5px;
  vertical-align: top;
}

#bxelbytvcn .gt_row_group_first td {
  border-top-width: 2px;
}

#bxelbytvcn .gt_summary_row {
  color: #333333;
  background-color: #FFFFFF;
  text-transform: inherit;
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
}

#bxelbytvcn .gt_first_summary_row {
  border-top-style: solid;
  border-top-color: #D3D3D3;
}

#bxelbytvcn .gt_first_summary_row.thick {
  border-top-width: 2px;
}

#bxelbytvcn .gt_last_summary_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#bxelbytvcn .gt_grand_summary_row {
  color: #333333;
  background-color: #FFFFFF;
  text-transform: inherit;
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
}

#bxelbytvcn .gt_first_grand_summary_row {
  padding-top: 8px;
  padding-bottom: 8px;
  padding-left: 5px;
  padding-right: 5px;
  border-top-style: double;
  border-top-width: 6px;
  border-top-color: #D3D3D3;
}

#bxelbytvcn .gt_striped {
  background-color: rgba(128, 128, 128, 0.05);
}

#bxelbytvcn .gt_table_body {
  border-top-style: solid;
  border-top-width: 2px;
  border-top-color: #D3D3D3;
  border-bottom-style: solid;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
}

#bxelbytvcn .gt_footnotes {
  color: #333333;
  background-color: #FFFFFF;
  border-bottom-style: none;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
}

#bxelbytvcn .gt_footnote {
  margin: 0px;
  font-size: 90%;
  padding-left: 4px;
  padding-right: 4px;
  padding-left: 5px;
  padding-right: 5px;
}

#bxelbytvcn .gt_sourcenotes {
  color: #333333;
  background-color: #FFFFFF;
  border-bottom-style: none;
  border-bottom-width: 2px;
  border-bottom-color: #D3D3D3;
  border-left-style: none;
  border-left-width: 2px;
  border-left-color: #D3D3D3;
  border-right-style: none;
  border-right-width: 2px;
  border-right-color: #D3D3D3;
}

#bxelbytvcn .gt_sourcenote {
  font-size: 90%;
  padding-top: 4px;
  padding-bottom: 4px;
  padding-left: 5px;
  padding-right: 5px;
}

#bxelbytvcn .gt_left {
  text-align: left;
}

#bxelbytvcn .gt_center {
  text-align: center;
}

#bxelbytvcn .gt_right {
  text-align: right;
  font-variant-numeric: tabular-nums;
}

#bxelbytvcn .gt_font_normal {
  font-weight: normal;
}

#bxelbytvcn .gt_font_bold {
  font-weight: bold;
}

#bxelbytvcn .gt_font_italic {
  font-style: italic;
}

#bxelbytvcn .gt_super {
  font-size: 65%;
}

#bxelbytvcn .gt_footnote_marks {
  font-style: italic;
  font-weight: normal;
  font-size: 75%;
  vertical-align: 0.4em;
}

#bxelbytvcn .gt_asterisk {
  font-size: 100%;
  vertical-align: 0;
}

#bxelbytvcn .gt_indent_1 {
  text-indent: 5px;
}

#bxelbytvcn .gt_indent_2 {
  text-indent: 10px;
}

#bxelbytvcn .gt_indent_3 {
  text-indent: 15px;
}

#bxelbytvcn .gt_indent_4 {
  text-indent: 20px;
}

#bxelbytvcn .gt_indent_5 {
  text-indent: 25px;
}
</style>
<table class="gt_table">
  
  <thead class="gt_col_headings">
    <tr>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col"></th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Player</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Team</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_left" rowspan="1" colspan="1" scope="col">Pos</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">Min</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">FIFA</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">FIFA_rating</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">Box</th>
      <th class="gt_col_heading gt_columns_bottom_border gt_right" rowspan="1" colspan="1" scope="col">box_rating</th>
    </tr>
  </thead>
  <tbody class="gt_table_body">
    <tr><th scope="row" class="gt_row gt_right gt_stub">1</th>
<td class="gt_row gt_left">Jeremy Ngakia</td>
<td class="gt_row gt_left">Watford</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">903</td>
<td class="gt_row gt_right">69</td>
<td class="gt_row gt_right" style="background-color: rgba(230,218,238,0.8); color: #000000;">-0.13144729</td>
<td class="gt_row gt_right">69.64005</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">-0.12464625</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">2</th>
<td class="gt_row gt_left">Shandon Baptiste</td>
<td class="gt_row gt_left">Brentford</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">910</td>
<td class="gt_row gt_right">66</td>
<td class="gt_row gt_right" style="background-color: rgba(238,230,243,0.8); color: #000000;">-0.17288570</td>
<td class="gt_row gt_right">70.38732</td>
<td class="gt_row gt_right" style="background-color: rgba(229,216,237,0.8); color: #000000;">-0.11385921</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">3</th>
<td class="gt_row gt_left">Chris Wood</td>
<td class="gt_row gt_left">Burnley</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2694</td>
<td class="gt_row gt_right">79</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">0.01453329</td>
<td class="gt_row gt_right">70.97824</td>
<td class="gt_row gt_right" style="background-color: rgba(185,149,206,0.8); color: #000000;">-0.09518406</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">4</th>
<td class="gt_row gt_left">Chris Wood</td>
<td class="gt_row gt_left">Newcastle Utd</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">2694</td>
<td class="gt_row gt_right">79</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">0.01453329</td>
<td class="gt_row gt_right">70.97824</td>
<td class="gt_row gt_right" style="background-color: rgba(185,149,206,0.8); color: #000000;">-0.09518406</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">5</th>
<td class="gt_row gt_left">Aaron Lennon</td>
<td class="gt_row gt_left">Burnley</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">1551</td>
<td class="gt_row gt_right">73</td>
<td class="gt_row gt_right" style="background-color: rgba(198,169,215,0.8); color: #000000;">-0.07654352</td>
<td class="gt_row gt_right">71.67621</td>
<td class="gt_row gt_right" style="background-color: rgba(152,112,179,0.8); color: #000000;">-0.09010116</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">6</th>
<td class="gt_row gt_left">Ashley Young</td>
<td class="gt_row gt_left">Aston Villa</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">1250</td>
<td class="gt_row gt_right">78</td>
<td class="gt_row gt_right" style="background-color: rgba(109,67,144,0.8); color: #FFFFFF;">-0.00644885</td>
<td class="gt_row gt_right">72.19038</td>
<td class="gt_row gt_right" style="background-color: rgba(147,106,175,0.8); color: #000000;">-0.08966248</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">7</th>
<td class="gt_row gt_left">Cucho</td>
<td class="gt_row gt_left">Watford</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">1147</td>
<td class="gt_row gt_right">75</td>
<td class="gt_row gt_right" style="background-color: rgba(185,149,206,0.8); color: #000000;">-0.04432508</td>
<td class="gt_row gt_right">72.11470</td>
<td class="gt_row gt_right" style="background-color: rgba(126,85,158,0.8); color: #FFFFFF;">-0.08795021</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">8</th>
<td class="gt_row gt_left">Mads Roerslev</td>
<td class="gt_row gt_left">Brentford</td>
<td class="gt_row gt_left">DF</td>
<td class="gt_row gt_right">1240</td>
<td class="gt_row gt_right">67</td>
<td class="gt_row gt_right" style="background-color: rgba(233,223,240,0.8); color: #000000;">-0.14916419</td>
<td class="gt_row gt_right">72.14783</td>
<td class="gt_row gt_right" style="background-color: rgba(79,37,120,0.8); color: #FFFFFF;">-0.08398980</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">9</th>
<td class="gt_row gt_left">Marc Albrighton</td>
<td class="gt_row gt_left">Leicester City</td>
<td class="gt_row gt_left">FW</td>
<td class="gt_row gt_right">1132</td>
<td class="gt_row gt_right">76</td>
<td class="gt_row gt_right" style="background-color: rgba(181,143,204,0.8); color: #000000;">-0.03443061</td>
<td class="gt_row gt_right">72.65074</td>
<td class="gt_row gt_right" style="background-color: rgba(59,15,104,0.8); color: #FFFFFF;">-0.08230763</td></tr>
    <tr><th scope="row" class="gt_row gt_right gt_stub">10</th>
<td class="gt_row gt_left">Jóhann Berg Guðmundsson</td>
<td class="gt_row gt_left">Burnley</td>
<td class="gt_row gt_left">MF</td>
<td class="gt_row gt_right">1102</td>
<td class="gt_row gt_right">75</td>
<td class="gt_row gt_right" style="background-color: rgba(187,152,208,0.8); color: #000000;">-0.04856484</td>
<td class="gt_row gt_right">72.45273</td>
<td class="gt_row gt_right" style="background-color: rgba(51,6,98,0.8); color: #FFFFFF;">-0.08168250</td></tr>
  </tbody>
  
  
</table>
</div>

---

# Model Comparison

## Relation

---

# Model Comparison

## Distribution

---

# Observation

## Position Value

---

# Discussion

##Future Work

- adding more data, increasing sample size to enhance model training and prediction accuracy
- employing more supervised learning techniques to increase prior model quality
- bagging to improve the stability and the accuracy of RAxGPM model
- choice of response variable: could we find a better measurement for soccer?
- implementing tracking data to build a more comprehensive model
- constructing Bayesian framework to add uncertainty to the model through distribution

## Applications

- predicting player’s market value and salary
- optimal line-up recommendation
- predicting game results and simulating league result
- evaluating players across different leagues

---

# References

- Hvattum, L. (2019). A comprehensive review of plus-minus ratings for evaluating individual players in team sports. International Journal of Computer Science in Sport.

- Matano, F., Richardson, L. F., Pospisil, T., Eubanks, C., & Qin, J. (2018). Augmenting adjusted plus-minus in soccer with FIFA ratings. arXiv preprint arXiv:1810.08032.

- Rosenbaum, D. T. (2004, April 30). Picking the difference makers for the All-NBA Teams. 82games.com. Retrieved July 28, 2022, from https://www.82games.com/comm30.html

- Sill, J. (2010). Improved NBA adjusted+/-using regularization and out-of-sample testing. In Proceedings of the 2010 MIT Sloan Sports Analytics Conference.

- Zhang, B., Tran Hoac, E., Hoang P. (2022). A RAPM Model for Soccer Player Ratings. https://www.stat.cmu.edu/cmsac/sure/2022/showcase/soccer_rapm.html

---

# Thanks!

<br />
[@GaryBoyuanZhang](https://twitter.com/GaryBoyuanZhang)